树与二叉树
1、树形结构
1.1、二叉树和多叉树
-
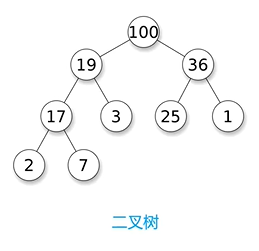
**二叉树:**指各节点的分叉数均不超过2的树。
-
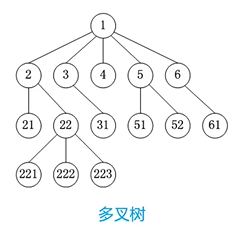
**多叉树:**指存在节点的分叉数超过2的树。
**注:**使用树形结构可以大大提高数据(或文件)增、删、改、查的效率。
1.2、树形结构的应用
如:
-
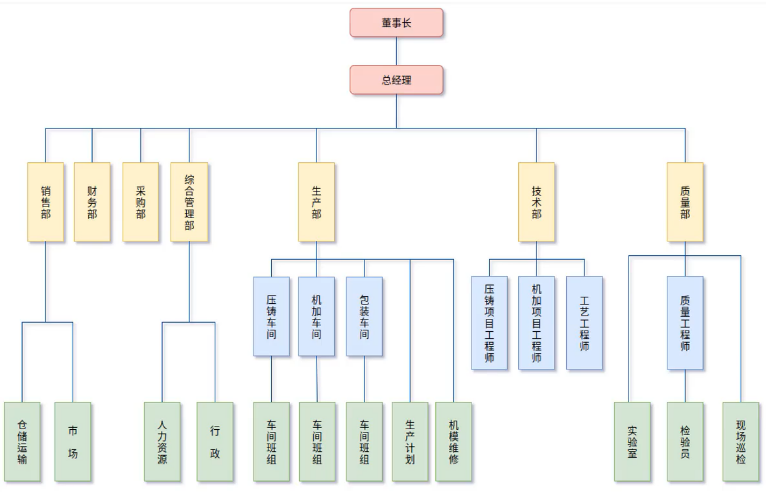
公司组织架构
-
文件夹组织架构
2、树(Tree)的基本概念
2.1、节点(node)
**节点:**指树的每一个数据元素。
2.1.1、根节点
根节点是树中唯一没有入边的节点。
2.1.2、父节点
一个节点是它出边所连接的所有节点的父节点。
2.1.3、子节点
一个节点是它入边所连接的节点的子节点。
2.1.4、叶子节点
没有子节点的节点称为叶子节点。
2.1.5、兄弟节点
具有相同父节点的节点互为兄弟节点。
如:上述多叉树中,21与22互为兄弟节点,21与31并不是兄弟节点。
注:
- 一棵树可以没有任何节点,称为**“空树”**。
- 一棵树最多只有一个根节点。
- 一棵树可以只有1个节点,即:只有根节点。
2.2、边(edge)
**边:**指连接两个节点的有向线段。
2.2.1、入边
**入边:**指从其它节点指向该节点的边。
2.2.2、出边
**出边:**指从该节点指向其它节点的边。
2.3、路径
**路径:**指由边连接起来的节点的有序排列。
2.4、空树
**空树:**指没有任何节点的树。
2.5、子树
一个节点的某个子节点的所有边和后代节点所构成的集合,称为该节点的子树。
2.5.1、左子树
二叉树指每个节点最多只能有两个子树的有序树。通常二叉树上某节点的左边子树称之为左子树。
2.5.2、右子树
二叉树上某节点的右边子树称之为右子树。
2.6、度(degree)
2.6.1、节点的度
节点的度:该节点子树的个数。
- 叶子节点:度为0的节点。
- 非叶子节点:度不为0的节点。
(二叉树:梅开二度)
2.6.2、树的度
树的度:所有节点的度中的最大值。
2.7、层数(level)
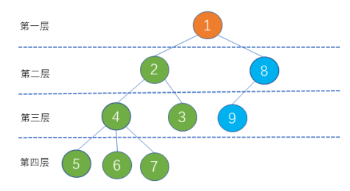
**层数:**从根节点到该节点的路径中的边的数目(+1)。
我们定义根节点为树的第一层,根节点的子节点为树的第二层,以此类推。
注:有的教材也从第0层开始计算,我们这里从第一层开始计算。
2.8、深度(depth)和高度(height)
2.8.1、节点的深度和高度
-
节点的深度:从根节点到当前节点的唯一路径上的节点总数。
-
节点的高度:从当前节点到最远叶子节点的路径上的节点总数。
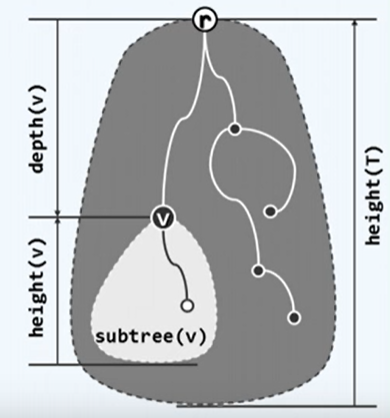
**注:**高度和深度计算的是节点数不是边数。
2.8.2、树的深度和高度
-
树的深度:所有节点深度中的最大值。
-
树的高度:所有节点高度中的最大值。
**注:**树的深度 = 树的高度。
2.9、有序树和无序树
2.9.1、有序树
**有序树:**树中任意节点的子节点之间有顺序关系。
注:
- 交换有序树中节点的位置,得到的是完全不同的两棵树。
- 我们后面使用的树,默认都是有序树。
2.9.2、无序树
**无序树:**树中任意节点的子节点之间没有顺序关系。
3、二叉树(Binary Tree)
3.1、二叉树的定义
**二叉树:**是指树中节点的度不大于2的有序树。
-
二叉树各节点的度均不超过2。(最多拥有2棵子树)
-
二叉树是有序树,其左子树和右子树是有顺序的,两者是不能任意交换顺序的。
**注:**即使某节点只有一棵子树,也要区分左右子树,不能任意交换顺序。
3.2、二叉树的性质
-
非空二叉树的第
i层,最多有个节点(i >= 1)。 -
在高度为
h的二叉树上最多有个节点(h >= 1)。
注: 。
- 对于任何一棵非空二叉树,如果叶子节点个数为,度为2的节点个数为,则。
**证:**假设度为1的节点个数为,那么二叉树的节点总数。
①度为2的节点的边数为2、度为1的节点的边数为1、叶子节点的边数为0;
②除根节点以外所有节点的顶部都有且只有一条边。
二叉树的边数,即。
注:
- 度为2的节点的出边边数为2、度为1的节点的出边边数为1、叶子节点的出边边数为0。
- 除根节点以外的所有节点的顶部都有且只有一条入边。
4、真二叉树(Proper Binary Tree)
**真二叉树:**所有节点的度均不为1的二叉树。(即:所有节点的度要么为0,要么为2。)
**注:**真二叉树是真“2”的二叉树。
5、满二叉树(Full Binary Tree)
5.1、概念
**满二叉树:**每一层的节点数都达到饱和状态的二叉树。
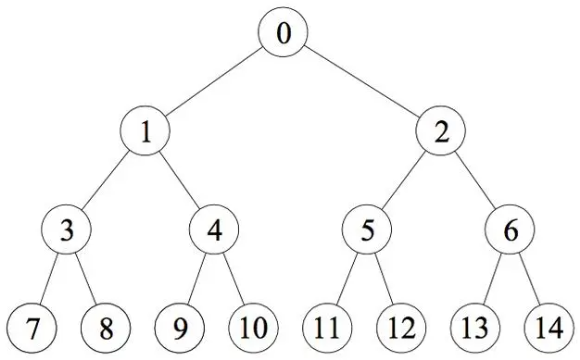
**注:**所有节点的度都要么为0,要么为2,且所有的叶子节点都在最后一层。
5.2、性质
-
在同样高度的二叉树中,满二叉树的叶子节点数量最多、总节点数量最多。
-
满二叉树一定是真二叉树,真二叉树不一定是满二叉树。
-
若满二叉树的高度为
h(h>= 1),则其第i层的节点数量为,叶子节点数量为,总节点数量。 -
若满二叉树的总节点数量为
n,则该满二叉树的高度 。
6、完全二叉树(Complete Binary Tree)
6.1、概念
**完全二叉树:**将满二叉树的最后一层从右往左依次删除若干个节点得到的二叉树。
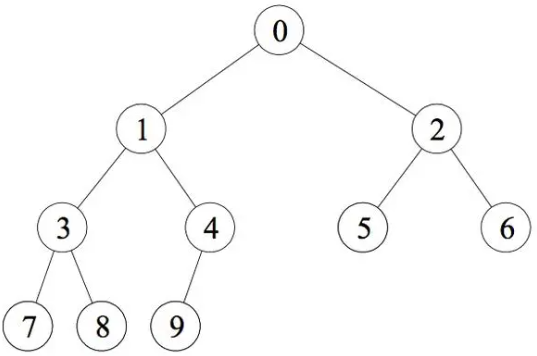
6.2、性质
-
叶子节点只会出现在最后两层,且最后一层的叶子节点都靠左对齐。
-
完全二叉树从第一层(根节点)至倒数第二层是一颗满二叉树。
-
满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树。
-
度为1的节点只有左子树。
-
度为1的节点数量要么是1个,要么是0个。
-
同样节点数量的二叉树,完全二叉树的高度最小。
-
若完全二叉树的高度为
h,则它:- 至少有个节点()。
- 最多有个节点(,满二叉树)。
- 总节点数量
n满足:,即:$h-1\le \log_2{n} \lt h $ 。
-
若完全二叉树的总节点数量为
n,则该完成二叉树的高度 ,其中为向下取整函数。 -
若完全二叉树的总节点数量为
n,则该完成二叉树的:- 叶子节点个数 ,
- 非叶子节点个数 。
其中为向下取整函数,为向上取整函数。
证: ,
又 要么是1个,要么是0个。
当时:n必须为偶数,,;
当时:n必须为奇数,,。
,
。
-
一棵有个节点的二叉树( ),按从上到下、从左到右的顺序从1开始依次对各节点进行编号,对任意第个节点有:
- 若 = 1,则它是根节点。
- 若,则它的父节点编号为,其中为向下取整函数。
- 若(即),则它的左子节点编号为。
- 若(即),则它没有左子节点。
- 若(即),则它的右子节点编号为。
- 若(即),则它没有右子节点。
-
一棵有个节点的二叉树(),按从上到下、从左到右的顺序从0开始依次对各节点进行编号,对任意第个节点有:
- 若 = 0,则它是根节点。
- 若 > 0,则它的父节点编号为,其中为向下取整函数。
- 若(即),则它的左子节点编号为。
- 若(即)),则它没有左子节点。
- 若(即),则它的右子节点编号为。
- 若(即),则它没有右子节点。
7、二叉树的存储和遍历
7.1、二叉树的存储
二叉树一般可以使用两种结构存储,一种是使用顺序结构存储,另一种是使用链式结构存储。
7.1.1、顺序存储
顺序结构存储就是使用数组来存储二叉树。
- 顺序存储适用于二叉树的形态和大小不发生剧烈变化的情况。
- 顺序存储可以使用一维数组进行实现,通过数组元素的下标作为索引,随机存取二叉树的节点元素。
(1)完全二叉树的顺序存储
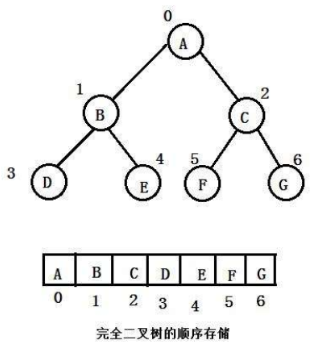
首先按照完全二叉树的层序顺序依次将数据存入一维数组。那么对于index=k的节点来说,它的左儿子为,右儿子为,如果发生越界则没有左儿子(或右儿子)。
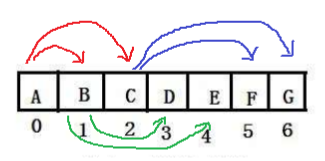
(2)非完全二叉树的顺序存储
对于一般的非完全二叉树,则将其补齐为完全二叉树。即:先将缺失的节点补上虚节点,然后再按照完全二叉树的方法进行顺序存储。
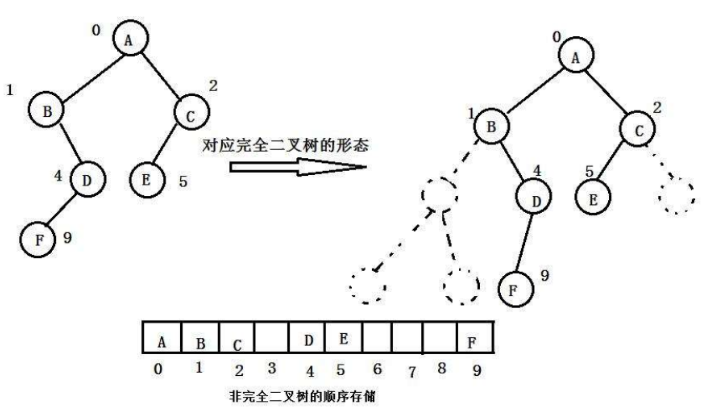
但是这种存储方法十分低效。尤其是当二叉树退化为线性结构时,会浪费很多的内存空间。
7.1.2、链式存储
(1)使用二叉链表存储
链式结构存储就是使用链表来存储二叉树。
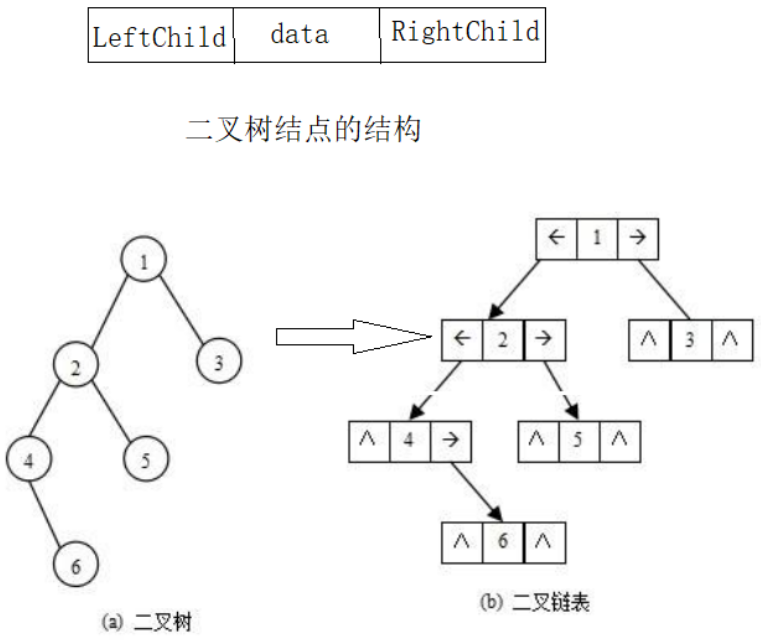
-
链式存储中每个结点一般由三部分组成:数据、左指针和右指针。(即使用二叉链表存储二叉树。)
其中,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。
-
链式存储只能通过迭代依次访问节点元素。
-
如果该节点没有左儿子(或右儿子),那么就将相应的指针赋值为
NULL。
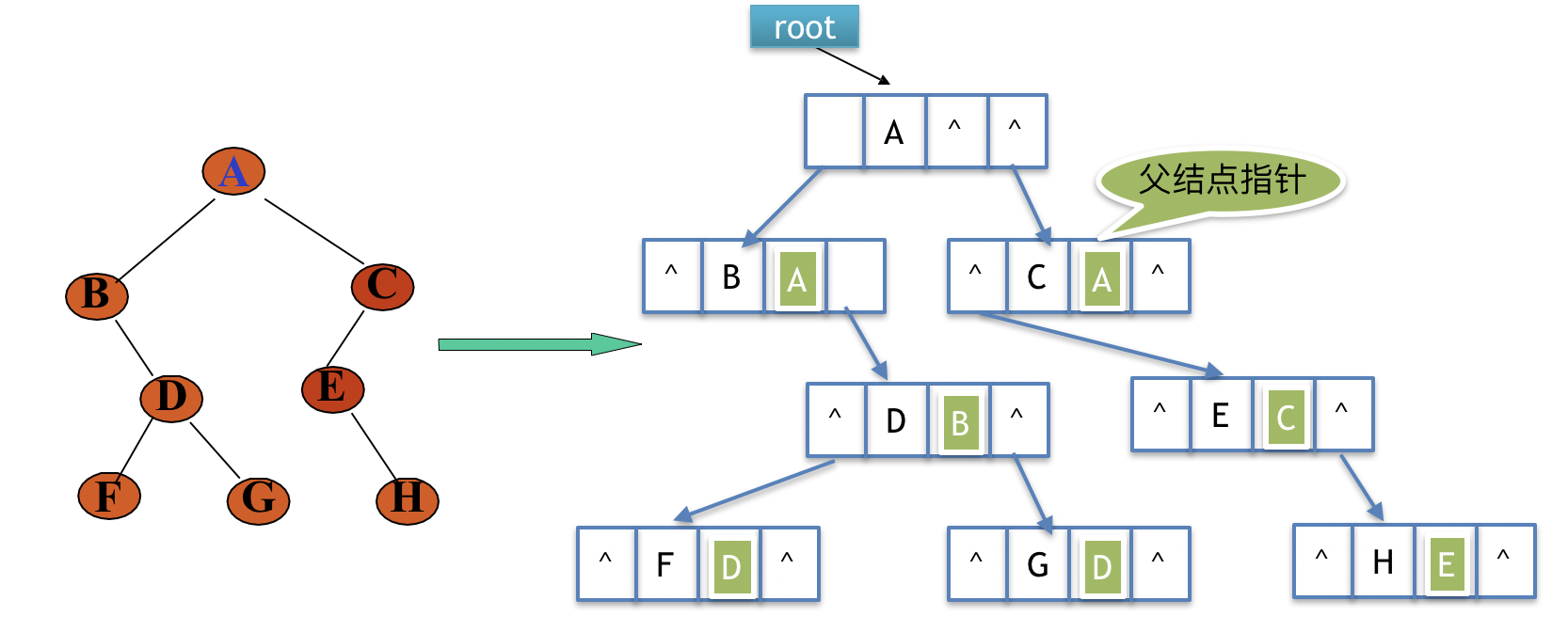
(2)使用三叉链表存储
为了方便找到当前结点的父结点,在设计二叉搜索树的每个结点的结构时,我们也可以添加一个指向父节点的指针。(即使用三叉链表存储二叉树。)
7.2、二叉树的遍历
7.2.1、定义
**遍历:**即把所有元素都访问一遍。
注:树的遍历过程等效于:将半线性的树形结构转换为线性结构。
7.2.2、遍历方式
根据节点访问顺序的不同,二叉树的常见遍历方式有4种(详见遍历二叉搜索树):
- 前序遍历(
Preorder Traversal) - 中序遍历(
Inorder Traversal) - 后序遍历(
Postorder Traversal) - 层序遍历(
Level Order Traversal)
**附:**线性数据结构的遍历比较简单,主要有:
- 正序遍历
- 逆序遍历
7.3、遍历的常见应用
(详见遍历二叉搜索树)
(本讲完,系列博文持续更新中…… )
参考文献:
[1] 《恋上数据结构与算法》,小码哥MJ
[2] 《数据结构与算法》,邓俊辉
如何获取源代码?
关注 “阿汤笔迹” 微信公众号,在后台回复关键词 “数据结构与算法设计与实现” ,即可获取项目源代码。
原文地址:http://www.atangbiji.com/2023/07/30/TreeAndBinaryTree/
博主最新文章在个人博客 http://www.atangbiji.com/ 发布。